Building Biomolecules, One Step At A Time

Understanding how eukaryotic cells synthesize glycan chains

Siddharth Kankaria | Illustrations by Dhanya Bharath

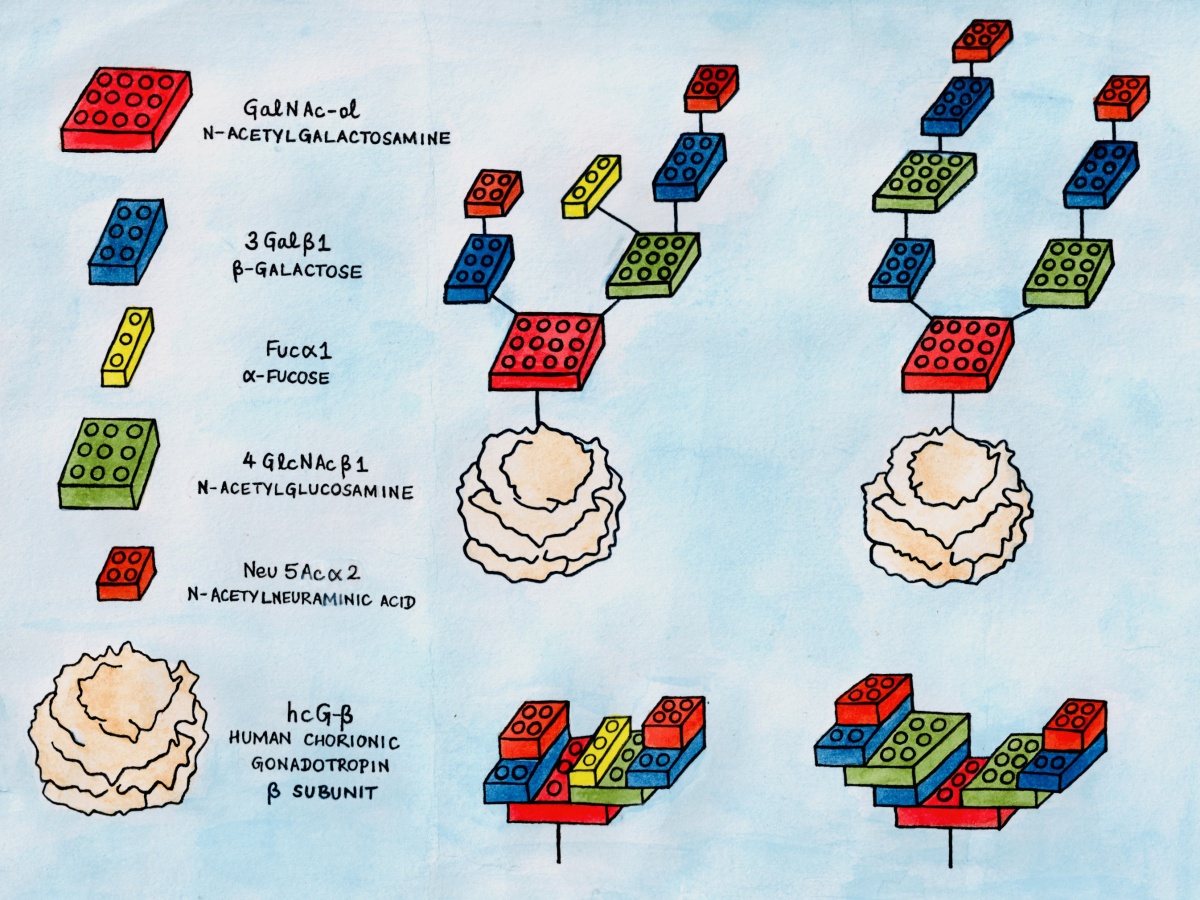
Glycan chains depicted as lego blocks

A fundamental process in biology is building larger structures using smaller building blocks.

Living systems have, over millennia, perfected the art of synthesizing macromolecules like DNA, RNA and proteins by using pre-existing templates, and proofreading them to remove errors. 

However, most biological structures are built using an algorithm or recipe, rather than a template. During embryonic development, recipes encoded in the organism’s genome are directly responsible for building complex structures like cells, tissues, organs and eventually the entire organism. 

Dr. Mukund Thattai – a computational cell biologist working at the Simons Centre for the Study of Living Machines at the National Centre for Biological Sciences, Bangalore – has been keenly interested in such algorithmic or step-by-step synthesis of biological structures.

He realised that glycan oligomers – branched sugar chains attached to proteins and lipids present on the surface of all living cells – could be the perfect system for studying algorithmic synthesis in biology.

Trained as a physicist, Thattai first learnt of glycobiology (the study of glycans and their biological roles) during his interaction with Prof. Ajit Varki, a physician-scientist at the University of California, San Diego, who’s been teaching a course on glycobiology at NCBS every alternate year since 2012.

“Ajit often calls glycobiology as the dark matter of biology”, recounts Thattai, “in the sense that it's everywhere, and plays important roles in a huge number of cellular processes, but is generally in the blind spot of most biologists”.

Building Glycans

The algorithmic synthesis of glycans is very similar to building Lego models: a small number of distinct building blocks (glycan monomers) can be assembled in various configurations to build a large diversity of Lego models (glycan chains).

These configurations are biologically made feasible partly because glycosyltransferases (the enzymes that create glycans) are doubly sloppy: they are both promiscuous (the ability to act on a set of different monomers within glycan chains without discrimination), as well as stochastic (the ability to add monomers to a glycan chain in random orders).

This means that in theory, these enzymes should be able to produce an astronomical array of glycan chains. Yet, only a small set of slightly variable glycan chains are found to be associated with cell surface proteins in eukaryotic cells.

These slight variations in glycan chains are termed microheterogeneity, and the repertoire of glycan chains associated with a eukaryotic protein is called its glycan profile.

The limited microheterogeneity of eukaryotic glycans has several important implications for life.

“Cell surface glycans act as cellular identity tags that enable cells to form sophisticated social networks, distinguish friends from foes, and advertise which species or tissue type they belong to”, explains Thattai. For example, the ABO blood groups that we are all familiar with are encoded by glycan chains present on the surface of red blood cells. Errors in these identity tags can lead to many sorts of disorders in cellular processes.

But, how are glycan profiles of proteins so tightly controlled in a eukaryotic cell?

Solving the mechanism

Thattai became very interested in finding the precise mechanism by which cells maintained such low levels of microheterogeneity while synthesizing glycan chains.

In 2014, he decided to pose an abstract glycan problem to Anjali Jaiman, a graduate student who has just joined him for a lab rotation. Together, they took a mathematical approach to model this biological process and posed the question: “how could one colour every node [glycan monomer] in a network [glycan chain], such that it was precisely constructible [synthesizable in a unique way]?” 

Anjali joined the lab as a PhD student and continued to work on this problem. It was around this time that Dr. Arnab Bhattacharyya, a theoretical computer scientist freshly recruited at the Indian Institute of Science, Bangalore, started visiting the Simons Centre at NCBS regularly, and became interested in the glycan problem.

Thattai reminisces that “Anjali, Arnab and I spent hours and hours of time over several weeks, trying to understand how to actually pose an interesting problem”, which is often the hardest part in designing a scientific study.

Real progress came when they decided to step away from the abstract mathematical models and start looking at real biological data. It didn’t take them long to figure out that “cells did not have enough colours (i.e. didn't have enough different types of sugars) to allow the observed glycan chains to be specifically assembled in our simplistic model”.

This insight led them to take a fresh approach, where they began to classify the different forms of glycan variability in eukaryotic cells.

In 2017, Jaiman decided to take a leave of absence from the doctoral program at NCBS and joined medical school in New York City, where she continues to pursue her medical degree currently. Thattai and Jaiman were only able to resume working on this problem during the summer of 2018 when Jaiman visited Bangalore for a few months.

“Over that summer, we spent every day of the week on this problem. On weekends, work shifted to the terrace of my flat, with my wife Nidhi keeping us well stocked with tea and cashew nuts. We went back to basics. Whenever we thought we had a solution, Anjali would come back the next morning with a counterexample: two steps forward, one step back or sideways. It was an intense, immersive mode of working”, narrates Thattai.

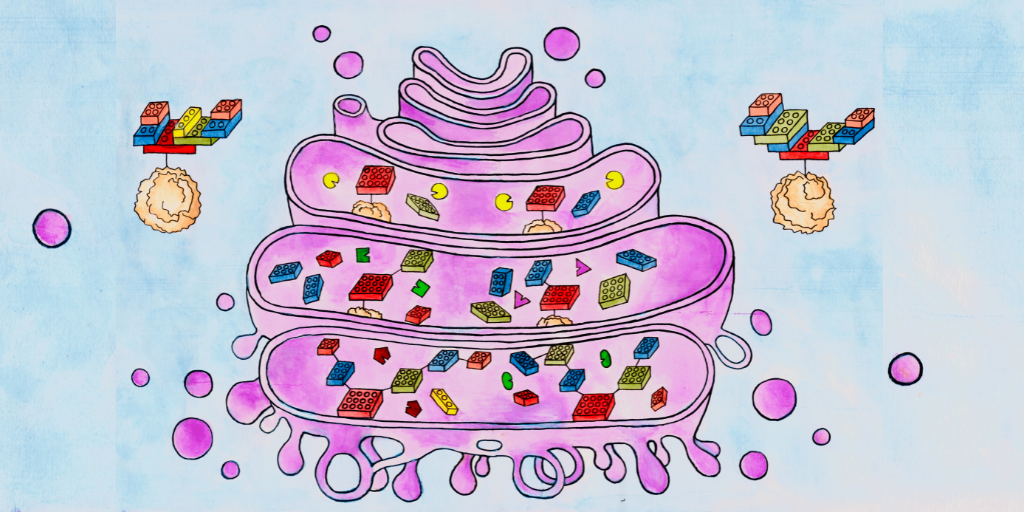
These sustained efforts soon started to bear fruit. As the outlines of a general theory gradually emerged, it struck them that the answer must lie in using multiple compartments to control the synthesis of glycan chains.

Building glycans in the Golgi, step-by-step

Golgi to the rescue

Interestingly, Thattai and Jaiman came to the realisation that the multi-compartment structure of the Golgi was relevant because the mathematical theory led them there. This was a classic case of theory and experiments synergistically reinforcing each other during the scientific process.

“The Golgi was staring us in the face all along, but we never focussed on that aspect. In retrospect it should have been obvious – the Golgi apparatus exists to do just one thing, make glycans”, explains Thattai.

They deduced that glycan oligomers could, in principle, grow algorithmically in sequential compartments of the Golgi apparatus by following simple incremental steps. This process of sequential and modular addition of components is called algorithmic growth and is very similar to an assembly line process used in a car factory.

For instance, it is more difficult (and energetically expensive) to re-train different factory workers (enzymes) to carry out different tasks (type of chemical synthesis). But, if different factory workers were trained to build specific car parts (specific glycan linkages), it is much easier to re-configure the sequence of factory workers on the assembly line (position of enzymes in the Golgi), and so build different car models or glycan chains.

Thattai & Jaiman realized that this was a classic example of “a quintessential eukaryotic trait (intracellular compartments) providing the means to overcome a fundamental biochemical limitation (promiscuous enzymes).” 

In July 2018, Thattai and Jaiman finally submitted a preprint paper (an article that is not yet peer-reviewed) to biorXiv, titled Algorithmic synthesis of eukaryotic glycans.

Soon after, Thattai got an opportunity to present their work at the acclaimed FEBS 2018 - Golgi Meeting in Italy, which is held every 10 years in honour of Camillo Golgi (the discoverer of the Golgi apparatus).

“This is one of those rare meetings in which both cell biologists (who know how the Golgi is assembled) and biochemists (who know how glycans are built) interact, and I learned a huge amount there”, narrates Thattai. They received a lot of critical inputs and feedback at this meeting and continued to fine-tune their study further.

“In early 2019, with my wife expecting a baby, I was spending a lot of time at home. Anjali was back in Bangalore for a visit, so we got a chance to get back to work. There was still one unfinished part of the puzzle because we had these two competing concepts: one was that cells could, under certain conditions, do perfect algorithmic synthesis; the other was that cells did, in practice, generate glycan variability. It turns out these concepts are connected: the algorithmic picture implies limits on how precisely real cells can synthesize glycans when enzymes are very promiscuous, and Golgi compartments too few”, shares Thattai.

After including all these new ideas, the paper was substantially different from the original preprint, and finally ready to submit to a journal. “Two days after my daughter was born”, recalls Thattai, “we submitted our manuscript to the journal eLife. A year and two revisions later, it was finally accepted in June 2020”.

Their study, Golgi compartments enable controlled biomolecular assembly using promiscuous enzymes, mathematically demonstrated that multi-compartment synthesis greatly increases the range of glycan chains that can be specifically produced by eukaryotic cells.

Looking ahead

Thattai feels that, among all the research projects he has participated in, this study stands out as involving the hardest journey from start to finish. “It was challenging because we took a long time to formulate the problem, understand the full scope, and find the right mathematical language”, explains Thattai. “But in the end, we actually reached the finish line, which is rare and therefore very satisfying.

He also feels that their work has set out a road map: “Our results are based on mathematical theorems, not computer simulations, so they are valid across different species and cell types. If people want to explore [different biological contexts], they just need to understand what algorithmic growth means for that context”.

Commenting on the implications of their study, Thattai explains that “the emergence of intracellular compartments was a watershed step in eukaryotic evolution. Our study has shown that the compartmental organization of the Golgi apparatus allows cells to control glycan synthesis despite enzymatic promiscuity, potentially explaining why this remarkable organelle is universally conserved across all eukaryotic lineages”.

The ability to control the assembly of small building blocks into large structures is of fundamental importance to both biology and engineering. According to Thattai, the results of this study could help improve the industrial production of therapeutic drugs; inspire strategies to precisely construct artificial nanomaterials in engineering applications; and help enable the field of quantitative glycomics to scale its growth, much like the fields of proteomics and lipidomics.

Most importantly, this study has helped clearly demonstrate that “the idea of the Golgi apparatus as a factory assembly line is more than a metaphor: it is a mathematical and biological necessity”, sums up Thattai.